Workshops Day 1

This morning I hung out at StreetFest and learned a bunch of stuff about category theory. First up was Ross Street who spoke about centres in monoidal categories. A monoidal category is essentially a category that carries a "monoid" structure, which may be thought of as a tensor product. An example from logic is the tensor product (conjunction) of linear logic. Or, if you prefer other language, the "fusion" of relevant logic. Or of Lambek Calculus or...

Here's a nice way to think about this. Suppose we only have the tensor-like conjunction. Then, a formula looks something like A ⊗ B ⊗ C. Represent each of A, B and C as a string connected between two bars. So, we have something that looks like:

The centre of this widget is all those formulae A such that A ⊗ X ≡ X ⊗ A for all other X. It turns out that the centre of a moinoidal category is always "braided". That means, if A and B are both in the centre and we go from A ⊗ B to B ⊗ A, then it matters whether we passed A "under" B or A "over" B. This corresponds to the following two situations for our strings:


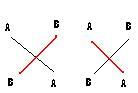
Remember that the strings are tied at the top and the bottom, so there is no way to pass from one "braiding" to the other (without cutting the strings of course!). Thus, the centre of a monoidal category forms a "braided" monoidal category. These crazy cats crop up all over the place. Quite famously, they are related to topological quantum field theories! The idea is that we imagine some particles (two say. Perhaps named A and B...) floating around in space (on a plane, say). Then, they can pass around each other in all sorts of fanciful ways. If we trace the history of where each particle has been, lo and behold we have a braiding!

As it happens, there are two ways to define a centre in a monoidal category. On the one hand, we can postulate a bunch of commutative diagrams which say that we can shift elements in the centre around however we please. This is called the "lax" centre. The other way is more refined and related to some constructions in algebra (which I have not fully grokked yet!). Essentially, each object, A, in the centre comes equipped with a bunch of "natural transformations", one for each object X in the category, which take A ⊗ X to X ⊗ A. Interestingly enough, these two notions of centre are not always the same (something I hadn't realised before today).

The other highlight of the categorical morning was Robin Cockett, who gave a beautiful talk about turning differential calculus into category theory! That is, we search for categorical analogues of "differentiable" and "smooth" functions. The idea is that we extend lambda calculus with the ability to do differentiation. Except, we do this in a category theoretic setting. This was quite a fun talk with lots of neat diagrams (no one can draw diagrams like a linear logician can!). Rather than waddle may way through discussing this stuff, I'll just point you to the paper (hot off the presses!) wherein all of this is done:

Differential Categories; R Blute, JRB Cockett, RAG Seely

I skipped out on the afternoon's categorical proceedings in order to hop along to the philosophical methodology workshop. Today's events were mainly devised for a group of visiting undergrads and had philosophers explaining their own take on general methodologies for doing philosophy. This was quite a nice insight into the philosophy world for me (since I am, after all, a philosophical neanderthal...). One of my motivations is that I would like to understand how people come up with conjectures and build arguments, so that I cant teach a computer to do the same! I managed to catch two of the talks. First up was Alan Hájek, who spoke about "Philosophical Heuristics". This was quite a neat talk explaining some general procedures for examining philosphical arguments in order to find bogus features. The general techniques are very familiar from maths, though there I think the situation is often a lot clearer since, for instance, definitions are clearly delineated! Quite amusingly, and rather contentiously by Canberra standards, his handout labelled nonclassical logics as weird... After that, Dave Chalmers spoke about "Terminological Disputes" - general ways of deciding whether an argument/disagreement is "terminological". That is, whether there is only a disagreement because the different parties parse a certain term differently.

Tomorrow I will once more hang out at StreetFest for part of the morning and then head over to see what else the philosphers have to say about methodology!